Getting Began with GNN Implementation

Introduction

In recent times, Graph Neural Networks (GNNs) have emerged as a potent device for analyzing and understanding graph-structured information. By leveraging the inherent construction and relationships inside graphs, GNNs provide a singular strategy to fixing a variety of machine studying duties. On this weblog, we’ll discover this idea from concept to GNN Implementation. From elementary rules to superior ideas, we’ll cowl all the pieces obligatory to know and successfully apply GNNs.

Studying Goal

• Perceive GNNs’ function in analyzing graph information.
• Discover node classification, hyperlink prediction, and graph era.
• Outline varieties like directed vs. undirected and weighted vs. unweighted.
• Create and visualize graphs utilizing Python libraries.
• Study its significance in GNNs for node communication.
• Discover GCNs, GATs, and graph pooling for environment friendly graph evaluation.

This text was revealed as part of the Knowledge Science Blogathon.

Why are GNNs Essential?

Conventional machine studying fashions, equivalent to convolutional neural networks (CNNs) and recurrent neural networks (RNNs), are designed to function on grid-like information constructions. Nevertheless, many real-world datasets, equivalent to social networks, quotation networks, and organic networks, exhibit a extra complicated construction represented by graphs. That is the place GNNs shine. They’re particularly tailor-made to deal with graph-structured information, making them well-suited for a wide range of functions.

Sensible Purposes of GNN

All through this weblog, we’ll discover a number of sensible functions of GNNs throughout totally different domains. A few of the functions we’ll cowl embrace:

1. Node Classification: Predicting properties or labels related to particular person nodes in a graph, equivalent to classifying customers in a social community based mostly on their pursuits.
2. Hyperlink Prediction: Anticipating lacking or future connections between nodes in a graph, equivalent to predicting potential interactions between proteins in a organic community.
3. Graph Classification: Classifying whole graphs based mostly on their structural properties, equivalent to categorizing molecular graphs by their chemical properties.
4. Graph Era: Producing new graphs that exhibit related properties to a given set of enter graphs, equivalent to creating life like social networks or molecular constructions.

Definition of Graphs

In arithmetic and laptop science, a graph is a information construction composed of nodes (also referred to as vertices) and edges (also referred to as hyperlinks or connections) that set up relationships between the nodes. Graphs are extensively used to mannequin and analyze relationships between entities in varied real-world situations

Varieties of Graphs

Graphs may be categorised into a number of varieties based mostly on totally different traits:

Directed vs. Undirected Graphs

In a directed graph, edges have a course related to them, indicating a one-way relationship between nodes. In distinction, undirected graphs have edges with none particular course, representing mutual relationships between nodes.

Weighted vs. Unweighted Graphs

In a weighted graph, every edge is assigned a numerical worth (weight) that represents the power or value of the connection between nodes. Unweighted graphs, however, don’t have such values related to edges.

Cyclic vs. Acyclic Graphs

A cyclic graph accommodates not less than one cycle, i.e., a sequence of edges that type a closed loop. In distinction, an acyclic graph doesn’t include any cycles.

Instance Dataset: Social Community Graph

For example dataset for hands-on exploration, let’s take into account a social community graph representing friendships between customers. On this graph:

• Nodes characterize particular person customers.
• Undirected edges characterize friendships between customers.
• Every node could have related attributes equivalent to consumer IDs, names, or pursuits.

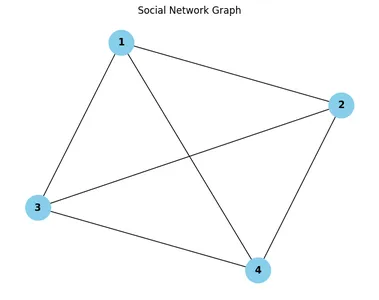
Right here’s a simplified illustration of a social community graph:

Nodes (Customers):     Edges (Friendships):
1 (Alice)          (1, 2), (1, 3), (1, 4)
2 (Bob)            (2, 3), (2, 4)
3 (Charlie)        (3, 4)
4 (David)

On this graph:

• Alice is associates with Bob, Charlie, and David.
• Bob is associates with Charlie and David.
• Charlie is associates with David.
• David has no extra associates on this community.

Now, let’s look right into a sensible hands-on exploration of the social community graph utilizing Python and the NetworkX library.

import networkx as nx
import matplotlib.pyplot as plt

# Create an empty undirected graph
social_network = nx.Graph()

# Add nodes representing customers
customers = [1, 2, 3, 4]
social_network.add_nodes_from(customers)

# Add edges representing friendships
friendships = [(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)]
social_network.add_edges_from(friendships)

# Visualize the social community graph
pos = nx.spring_layout(social_network)  # Positions for all nodes
nx.draw(social_network, pos, with_labels=True, node_color="skyblue", node_size=1000,
font_size=12, font_weight="daring")
plt.title("Social Community Graph")
plt.present()

Within the code above:

• We first import the NetworkX library, which supplies instruments for working with graphs.
• We create an empty undirected graph named social_network.
• We add nodes representing particular person customers utilizing their distinctive IDs.
• We add edges representing friendships between customers based mostly on the supplied checklist of friendships.
• Lastly, we visualize the social community graph utilizing the nx.draw() operate, specifying node positions, labels, colours, and different visible attributes.

Decoding the Social Community Graph

Within the visible illustration of the social community graph, every node corresponds to a consumer, and every edge represents a friendship between customers. By inspecting the graph, we will infer varied insights:

1. Node Illustration: Every node is labeled with a singular consumer ID, permitting us to establish particular person customers inside the community.
2. Edge Illustration: Edges connecting nodes point out mutual friendships between customers. For instance, if there’s an edge between nodes 1 and a couple of, it implies that consumer 1 and consumer 2 are associates.
3. Community Construction: By observing the general construction of the graph, we will establish clusters of customers who’re interconnected by means of mutual friendships.

Past visible inspection, we will carry out extra evaluation and exploration on the social community graph utilizing NetworkX and different Python libraries. Listed below are some examples of what you are able to do:

Node Diploma

Calculate the diploma of every node, which represents the variety of friendships related to that consumer.

# Calculate node levels
node_degrees = dict(social_network.diploma())
print("Node Levels:", node_degrees)

Linked Parts

Establish linked elements inside the graph, representing teams of customers who’re mutually linked by means of friendships.

# Discover linked elements
connected_components = checklist(nx.connected_components(social_network))
print("Linked Parts:", connected_components)

 Shortest Paths

Discover the shortest path between two customers, indicating the minimal variety of friendships required to attach them.

# Discover shortest path between two customers
shortest_path = nx.shortest_path(social_network, supply=1, goal=4)
print("Shortest Path from Person 1 to Person 4:", shortest_path)

Limitations of Conventional Machine Studying Approaches with Graph Knowledge

Conventional machine studying approaches, equivalent to convolutional neural networks (CNNs) and recurrent neural networks (RNNs), are designed to function successfully on grid-like information constructions, equivalent to photos, sequences, and tabular information. Nevertheless, these approaches face vital limitations when utilized to graph-structured information:

1. Permutation Invariance: Conventional fashions lack permutation invariance, that means they deal with inputs as fixed-size vectors or sequences with out contemplating the inherent permutation of nodes in a graph. In consequence, they battle to successfully seize the complicated relationships and dependencies inside graphs.
2. Variable-Sized Inputs: Graphs can have various numbers of nodes and edges, making it difficult to course of them utilizing fixed-size architectures. Conventional fashions usually require preprocessing methods, equivalent to graph discretization or graph embedding, which can result in info loss or computational inefficiency.
3. Native vs. World Info: Conventional fashions sometimes give attention to capturing native info inside neighborhoods or sequences, however they might battle to include world info that spans the complete graph. This limitation can hinder their capacity to make correct predictions or classifications based mostly on the holistic construction of the graph.
4. Graph-Dependent Construction: Graph-structured information reveals a wealthy, interconnected construction with heterogeneous node and edge attributes. Conventional fashions should not inherently outfitted to deal with this complicated construction, resulting in suboptimal efficiency and generalization on graph-related duties.

Introducing Graph Neural Networks (GNNs) as a Answer

Graph Neural Networks (GNNs) provide a strong answer to beat the restrictions of conventional machine studying approaches when working with graph-structured information. GNNs lengthen neural community architectures to instantly function on graph-structured inputs, enabling them to successfully seize and course of info from nodes and edges inside the graph.

Key options and benefits of GNNs embrace:

1. Graph Illustration Studying: GNNs be taught distributed representations (embeddings) for nodes and edges within the graph, permitting them to encode each structural and attribute info inside a unified framework.
2. Message Passing: GNNs leverage message passing algorithms to propagate info between neighboring nodes within the graph. By iteratively aggregating and updating node representations based mostly on native neighborhood info, GNNs can seize complicated dependencies and relational patterns inside the graph.
3. Permutation Invariance: GNNs inherently account for the permutation of nodes inside a graph, making certain that they function constantly no matter node ordering. This property permits GNNs to keep up spatial consciousness and successfully mannequin graph-structured information with out the necessity for express preprocessing.
4. Scalability and Flexibility: GNNs are extremely scalable and versatile, able to dealing with graphs of various sizes and constructions. They are often tailored to several types of graph-related duties, together with node classification, hyperlink prediction, graph classification, and graph era.

Fundamentals of Graph Neural Networks

Graph Illustration

Graph illustration is a elementary facet of Graph Neural Networks (GNNs), because it entails encoding the construction and attributes of a graph right into a format appropriate for computational processing. On this part, we’ll discover learn how to characterize graphs utilizing fashionable libraries equivalent to NetworkX and PyTorch Geometric, together with code snippets for creating and visualizing graphs.

Illustration Utilizing NetworkX

NetworkX is a Python library for creating, manipulating, and learning complicated networks, together with graphs. It supplies a handy interface for constructing graphs and performing varied graph operations.

import networkx as nx
import matplotlib.pyplot as plt

# Create an empty undirected graph
G = nx.Graph()

# Add nodes
G.add_node(1)
G.add_node(2)
G.add_node(3)

# Add edges
G.add_edge(1, 2)
G.add_edge(2, 3)

# Visualize the graph
nx.draw(G, with_labels=True)
plt.title("Graph Illustration Utilizing NetworkX")
plt.present()

Illustration Utilizing PyTorch Geometric

PyTorch Geometric is a library for deep studying on irregular enter information, equivalent to graphs, with assist for environment friendly batching and GPU acceleration.

# set up torch-geometric 
!pip set up torch-geometric -f https://pytorch-geometric.com/whl/torch-1.9.0+cu111.html

# import libraries
import torch
from torch_geometric.information import Knowledge
from torch_geometric.utils import to_networkx
import matplotlib.pyplot as plt
import networkx as nx

# Outline edge indices and node options
edge_index = torch.tensor([[0, 1], [1, 2]], dtype=torch.lengthy)
x = torch.tensor([[1], [2], [3]], dtype=torch.float)

# Create a PyTorch Geometric Knowledge object
information = Knowledge(x=x, edge_index=edge_index.t().contiguous())

# Convert to NetworkX graph
G = to_networkx(information)

# Visualize the graph
nx.draw(G, with_labels=True)
plt.title("Graph Illustration Utilizing PyTorch Geometric")
plt.present()

In each examples, we’ve created a easy graphs with three nodes and two edges. Nevertheless, the strategies of graph illustration differ barely between NetworkX and PyTorch Geometric.

NetworkX Illustration

• In NetworkX, nodes and edges are added individually utilizing add_node() and add_edge() strategies.
• The visualization of the graph is simple, with nodes represented as circles and edges as traces connecting them.

PyTorch Geometric Illustration

• PyTorch Geometric represents graphs utilizing specialised information constructions tailor-made for deep studying duties.
• Node options and edge connectivity are encapsulated inside a Knowledge object, offering a extra structured illustration.
• PyTorch Geometric integrates seamlessly with PyTorch, making it appropriate for graph-based deep studying duties.

Interpretation

• Each representations serve their respective functions, NetworkX is well-suited for graph evaluation and visualization duties, whereas PyTorch Geometric supplies a framework for deep studying on graphs.
• Relying on the duty at hand, you may select the suitable illustration and library. For conventional graph algorithms and visualization, NetworkX could also be preferable. For deep studying duties involving graphs, PyTorch Geometric affords extra flexibility and effectivity.

Message Passing

In Graph Neural Networks (GNNs), message passing is a elementary idea that enables nodes in a graph to speak with one another. Consider it like passing notes at school – every node sends a message to its neighbors, after which all of them replace their info based mostly on these messages.

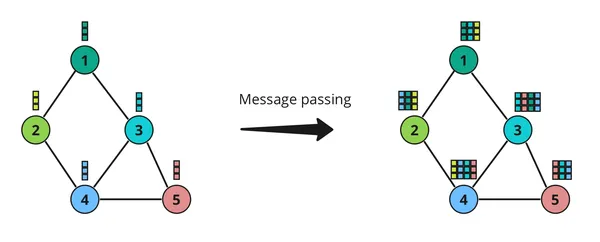
Right here’s The way it Works

1. Sending Messages: Every node gathers info from its neighbors and sends out a message. This message sometimes accommodates details about the node itself and its neighbors.
2. Receiving Messages: As soon as a node receives messages from its neighbors, it combines this info with its personal and updates its inside illustration. This step helps the node perceive its place within the bigger graph.
3. Updating Info: After receiving messages from neighbors, every node updates its personal info based mostly on these messages. This replace course of ensures that every node has a extra full understanding of the graph’s construction and properties.

Message passing is essential in GNNs as a result of it permits nodes to leverage info from their native neighborhoods to make knowledgeable choices. It’s like neighbors sharing gossip – by exchanging messages, nodes can collectively acquire insights into the general construction and dynamics of the graph. This allows GNNs to carry out duties equivalent to node classification, hyperlink prediction, and graph classification successfully.

Implementing Message Passing in Python

To implement a easy message passing algorithm in Python, we’ll create a primary Graph Neural Community (GNN) layer that performs message passing between neighboring nodes and updates node representations. Let’s use a toy graph with randomly initialized node options and adjacency matrix for demonstration functions.

import numpy as np

# Outline a toy graph with 4 nodes and their preliminary options
num_nodes = 4
num_features = 2
adjacency_matrix = np.array([[0, 1, 0, 1],
                             [1, 0, 1, 1],
                             [0, 1, 0, 0],
                             [1, 1, 0, 0]])  # Adjacency matrix

node_features = np.random.rand(num_nodes, num_features)  # Random node options

# Outline a easy message passing operate
def message_passing(adj_matrix, node_feats):
    updated_feats = np.zeros_like(node_feats)
    num_nodes = len(node_feats)
    
    # Iterate over every node
    for i in vary(num_nodes):
        # Collect neighboring nodes based mostly on adjacency matrix
        neighbors = np.the place(adj_matrix[i] == 1)[0]
        
        # Combination messages from neighbors
        message = np.sum(node_feats[neighbors], axis=0)
        
        # Replace node illustration
        updated_feats[i] = node_feats[i] + message
    
    return updated_feats

# Carry out message passing for one iteration
updated_features = message_passing(adjacency_matrix, node_features)
print("Up to date Node Options after Message Passing:")
print(updated_features)

# output
#Up to date Node Options after Message Passing:
#[[0.5602586  1.54137027]
# [0.61232074 1.59538215]
# [0.28878133 0.69739586]
#[0.5602586  1.54137027]]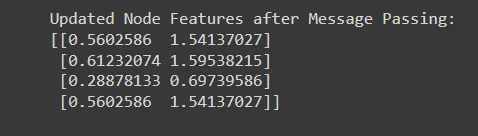

On this code:

• We outline a toy graph with 4 nodes and their preliminary options, represented by a random matrix for node options and an adjacency matrix for edges.
• We create a easy message passing operate (message_passing) that iterates over every node, gathers messages from neighboring nodes based mostly on the adjacency matrix, and updates node representations by aggregating messages.
• We carry out one iteration of message passing on the toy graph and print the up to date node options.
• The message_passing operate iterates over every node within the graph and gathers messages from its neighboring nodes.
• The neighbors variable shops the indices of neighboring nodes based mostly on the adjacency matrix.
• The message variable aggregates node options from neighboring nodes.
• The node illustration is up to date by including the message to the unique node options.
• This course of is repeated for every node, leading to up to date node representations after one iteration of message passing.

Extending Message Passing for Advanced Relationships

Let’s lengthen the instance to carry out a number of iterations of message passing to seize extra complicated relationships inside the graph.

# Outline the variety of message passing iterations
num_iterations = 3

# Carry out a number of iterations of message passing
for _ in vary(num_iterations):
    node_features = message_passing(adjacency_matrix, node_features)

print("Up to date Node Options after A number of Iterations of Message Passing:")
print(node_features)

# output
# Up to date Node Options after A number of Iterations of Message Passing:
#[[ 5.48729515 14.73176393]
# [ 6.38839722 17.02454194]
# [ 2.92272134  7.66829656]
# [ 5.48729515 14.73176393]]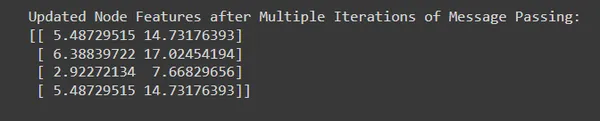

• By performing a number of iterations of message passing, we permit info to propagate and accumulate throughout the graph, capturing more and more complicated relationships and dependencies.
• Every iteration refines the node representations based mostly on info aggregated from neighboring nodes, resulting in progressively enhanced node embeddings.

Graph Convolutional Networks (GCNs)

Graph Convolutional Networks (GCNs), the superheroes of the machine studying world, outfitted with the superpower to navigate and extract insights from these tangled webs. GCNs should not simply one other algorithm; they’re a revolutionary strategy that revolutionizes how we analyze and perceive graph-structured information. In Graph Neural Networks (GNNs), Graph Convolutional Networks (GCNs) are a particular sort of mannequin designed to function on graph-structured information. GCNs are impressed by convolutional neural networks (CNNs) utilized in picture processing, however tailored to deal with the irregular and non-Euclidean construction of graphs.

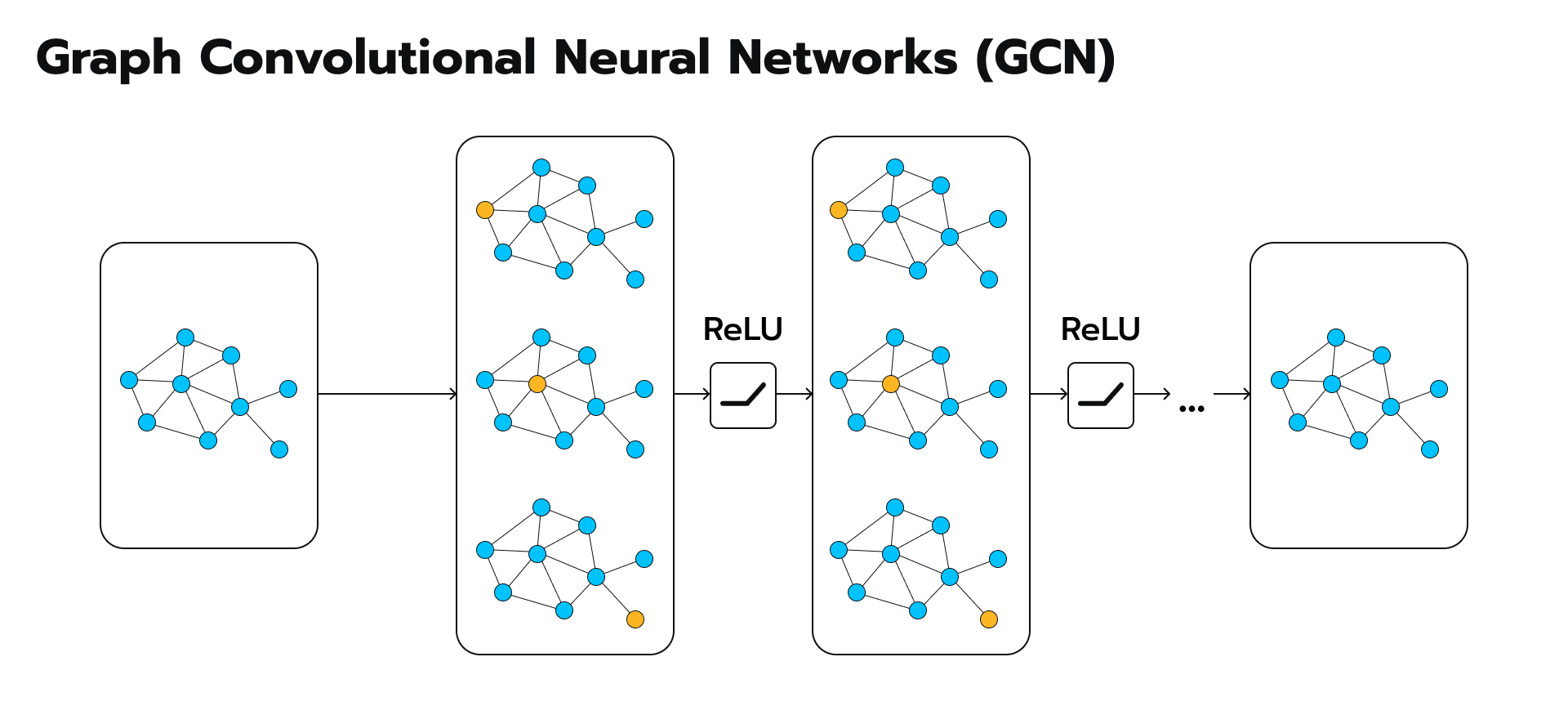
Right here’s a simplified rationalization

• Understanding Graphs: In lots of real-world situations, information may be represented as a graph, the place entities (nodes) are linked by relationships (edges). For instance, in a social community, individuals are nodes, and friendships are edges.
• What GCNs Do: GCNs goal to be taught helpful representations of nodes in a graph by bearing in mind the options of neighboring nodes. They do that by propagating info by means of the graph utilizing a course of known as message passing.
• Message Passing: At every layer of a GCN, nodes mixture info from their neighbors, sometimes by taking a weighted sum of their options. This aggregation course of is akin to a node gathering info from its rapid environment.
• Studying Representations: By a number of layers of message passing, GCNs be taught more and more summary representations of nodes that seize each native and world graph constructions. These representations can then be used for varied downstream duties, equivalent to node classification, hyperlink prediction, or graph classification.
• Coaching: Like different neural networks, GCNs are educated utilizing labeled information, the place the mannequin learns to foretell node labels or different properties of curiosity based mostly on enter graph information.

GCNs are highly effective instruments for studying from graph-structured information, enabling duties equivalent to node classification, hyperlink prediction, and graph-level prediction in a wide range of domains, together with social networks, organic networks, and advice methods.

Instance of a GCN Mannequin

Let’s outline a easy GCN mannequin with two graph convolutional layers to know higher.

import time
import torch
import torch.nn.purposeful as F
import torch_geometric.transforms as T
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import GCNConv


if torch.cuda.is_available():
    machine = torch.machine('cuda')
elif hasattr(torch.backends, 'mps') and torch.backends.mps.is_available():
    machine = torch.machine('mps')
else:
    machine = torch.machine('cpu')


class GCN(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels):
        tremendous().__init__()
        self.conv1 = GCNConv(in_channels, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, out_channels)

    def ahead(self, x, edge_index, edge_weight=None):
        x = F.dropout(x, p=0.5, coaching=self.coaching)
        x = self.conv1(x, edge_index, edge_weight).relu()
        x = F.dropout(x, p=0.5, coaching=self.coaching)
        x = self.conv2(x, edge_index, edge_weight)
        return x

We’ll use the Cora dataset, a quotation community. PyTorch Geometric supplies built-in capabilities to obtain and preprocess fashionable datasets.

#dataset

dataset = Planetoid(root="information", title="Cora", rework=T.NormalizeFeatures())
information = dataset[0].to(machine)


rework = T.GDC(
    self_loop_weight=1,
    normalization_in='sym',
    normalization_out="col",
    diffusion_kwargs=dict(technique='ppr', alpha=0.05),
    sparsification_kwargs=dict(technique='topk', okay=128, dim=0),
    precise=True,
)
information = rework(information)

We’ll prepare the GCN mannequin on the Cora dataset utilizing commonplace coaching procedures.

mannequin = GCN(
    in_channels=dataset.num_features,
    hidden_channels=16,
    out_channels=dataset.num_classes,
).to(machine)

optimizer = torch.optim.Adam([
    dict(params=model.conv1.parameters(), weight_decay=5e-4),
    dict(params=model.conv2.parameters(), weight_decay=0)
], lr=0.01)  # Solely carry out weight-decay on first convolution.


def prepare():
    mannequin.prepare()
    optimizer.zero_grad()
    out = mannequin(information.x, information.edge_index, information.edge_attr)
    loss = F.cross_entropy(out[data.train_mask], information.y[data.train_mask])
    loss.backward()
    optimizer.step()
    return float(loss)
    
@torch.no_grad()
def take a look at():
    mannequin.eval()
    pred = mannequin(information.x, information.edge_index, information.edge_attr).argmax(dim=-1)

    accs = []
    for masks in [data.train_mask, data.val_mask, data.test_mask]:
        accs.append(int((pred[mask] == information.y[mask]).sum()) / int(masks.sum()))
    return accs

Coaching until 20 epochs

best_val_acc = test_acc = 0
occasions = []
for epoch in vary(1, 20 + 1):
    begin = time.time()
    loss = prepare()
    train_acc, val_acc, tmp_test_acc = take a look at()
    if val_acc > best_val_acc:
        best_val_acc = val_acc
        test_acc = tmp_test_acc
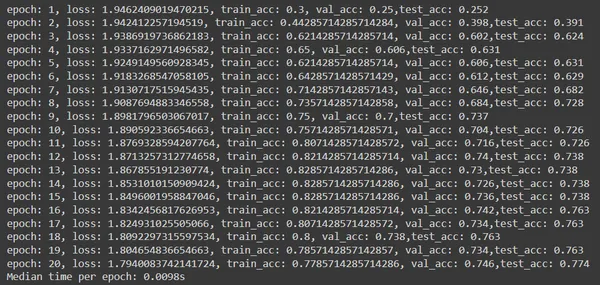
    print(f"epoch: {epoch}, loss: {loss}, train_acc: {train_acc}, val_acc: {val_acc},
    test_acc: {test_acc}")
    occasions.append(time.time() - begin)
print(f'Median time per epoch: {torch.tensor(occasions).median():.4f}s')

Rationalization

• The code begins by importing obligatory libraries together with time, torch, torch.nn.purposeful (usually imported as F), and elements from torch_geometric together with transforms, datasets, and neural community modules.
• It checks if CUDA is obtainable for GPU computation; if not, it checks for the supply of the Multi-Course of Service (MPS). If neither is obtainable, it defaults to CPU.
• The code masses the Cora dataset from the Planetoid dataset assortment in PyTorch Geometric. It normalizes the options and masses the dataset onto the desired machine (CPU or GPU).
• It applies a Graph Diffusion Convolution (GDC) transformation to the dataset. GDC is a pre-processing step that enhances the illustration of the graph construction.
• A Graph Convolutional Community (GCN) mannequin is outlined utilizing PyTorch’s torch.nn.Module class. It consists of two GCN layers (GCNConv) adopted by ReLU activation and dropout layers.
• An Adam optimizer is outlined to optimize the parameters of the GCN mannequin. Weight decay is utilized to the parameters of the primary convolutional layer solely.
• The prepare operate is outlined to coach the GCN mannequin. It units the mannequin to coaching mode, computes the output, calculates the loss utilizing cross-entropy, performs backpropagation, and updates the parameters utilizing the optimizer.
• The take a look at operate evaluates the educated mannequin on the coaching, validation, and take a look at units. It computes predictions, calculates accuracy for every set, and returns the accuracies.
• The code iterates by means of 20 epochs, calling the prepare operate to coach the mannequin and the take a look at operate to guage it on the validation and take a look at units. It additionally tracks the perfect validation accuracy and corresponding take a look at accuracy.
• The outcomes together with epoch quantity, loss, coaching accuracy, validation accuracy, and take a look at accuracy are printed for every epoch. Additionally, the median time taken per epoch is computed and printed on the finish of coaching.

Graph Consideration Networks (GATs)

Graph Consideration Networks (GATs) are a sort of Graph Neural Community (GNN) structure that introduces consideration mechanisms to be taught node representations in a graph. Consideration mechanisms have been extensively profitable in pure language processing duties, permitting fashions to give attention to related elements of enter sequences. GATs lengthen this concept to graphs, enabling the mannequin to dynamically weigh the significance of neighboring nodes’ options when aggregating info.

The important thing concept behind GATs is to compute consideration scores between a central node and its neighbors, that are then used to compute weighted function representations of the neighbors. These weighted representations are aggregated to provide an up to date illustration of the central node. By studying these consideration scores throughout coaching, GATs can successfully seize the significance of various neighbors for every node within the graph.

One of many predominant benefits of GATs is their capacity to seize complicated relationships and dependencies between nodes within the graph. Not like conventional GNN architectures that use fastened aggregation capabilities, GATs can adaptively assign larger weights to extra related neighbors, resulting in extra expressive node representations.

Right here’s a breakdown of GATs

• Consideration Mechanisms: Impressed by the eye mechanism generally utilized in pure language processing, GATs assign totally different consideration scores to every neighbor of a node. This permits the mannequin to give attention to extra related neighbors whereas aggregating info.
• Studying Weights: As a substitute of utilizing fastened weights for aggregating neighbors’ options, GATs be taught these weights dynamically throughout coaching. Which means the mannequin can adaptively assign larger significance to nodes which are extra related to the present job.
• Multi-Head Consideration: GATs usually make use of a number of consideration heads, every studying a distinct set of weights. This allows the mannequin to seize totally different features of the relationships between nodes and helps enhance efficiency.
• Illustration Studying: Like different GNNs, GATs goal to be taught significant representations of nodes in a graph. By leveraging consideration mechanisms, GATs can seize complicated patterns and dependencies within the graph construction, resulting in extra expressive node embeddings.

Instance of a GAT Mannequin

Let’s create a GAT-based mannequin structure utilizing the outlined Graph Consideration Layer.

import time
import torch
import torch.nn.purposeful as F
import torch_geometric.transforms as T
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import GATConv

machine = torch.machine('cuda' if torch.cuda.is_available() else 'cpu')

class GAT(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels, heads):
        tremendous().__init__()
        self.conv1 = GATConv(in_channels, hidden_channels, heads, dropout=0.6)
        # On the Pubmed dataset, use `heads` output heads in `conv2`.
        self.conv2 = GATConv(hidden_channels * heads, out_channels, heads=1,
                             concat=False, dropout=0.6)

    def ahead(self, x, edge_index):
        x = F.dropout(x, p=0.6, coaching=self.coaching)
        x = F.elu(self.conv1(x, edge_index))
        x = F.dropout(x, p=0.6, coaching=self.coaching)
        x = self.conv2(x, edge_index)
        return x

We’ll once more use the Cora dataset.

dataset = Planetoid(root="information", title="Cora", rework=T.NormalizeFeatures())
information = dataset[0].to(machine)

hidden_channels=8
heads=8
lr=0.005
epochs=10

mannequin = GAT(dataset.num_features, hidden_channels, dataset.num_classes,
            heads).to(machine)
optimizer = torch.optim.Adam(mannequin.parameters(), lr=0.005, weight_decay=5e-4)

Coaching GAT until 10 epochs

def prepare():
    mannequin.prepare()
    optimizer.zero_grad()
    out = mannequin(information.x, information.edge_index)
    loss = F.cross_entropy(out[data.train_mask], information.y[data.train_mask])
    loss.backward()
    optimizer.step()
    return float(loss)


@torch.no_grad()
def take a look at():
    mannequin.eval()
    pred = mannequin(information.x, information.edge_index).argmax(dim=-1)

    accs = []
    for masks in [data.train_mask, data.val_mask, data.test_mask]:
        accs.append(int((pred[mask] == information.y[mask]).sum()) / int(masks.sum()))
    return accs


occasions = []
best_val_acc = final_test_acc = 0
for epoch in vary(1, epochs + 1):
    begin = time.time()
    loss = prepare()
    train_acc, val_acc, tmp_test_acc = take a look at()
    if val_acc > best_val_acc:
        best_val_acc = val_acc
        test_acc = tmp_test_acc
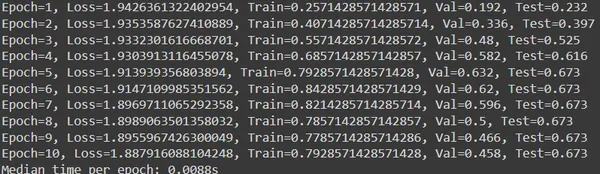
    print(f"Epoch={epoch}, Loss={loss}, Prepare={train_acc}, Val={val_acc}, Take a look at={test_acc}")
    occasions.append(time.time() - begin)
print(f"Median time per epoch: {torch.tensor(occasions).median():.4f}s")

Code Rationalization:

• Import obligatory libraries: time, torch, torch.nn.purposeful (F), torch_geometric.transforms (T), torch_geometric.datasets.Planetoid, and torch_geometric.nn.GATConv, tailor-made for graph consideration networks.
• Verify for CUDA availability; set machine to ‘cuda’ if out there, else default to ‘cpu’.
• Outline GAT mannequin as a torch.nn.Module subclass. Initialize mannequin’s layers, together with two GATConv layers. Ahead technique passes enter options (x) and edge indices by means of GATConv layers.
• Load Cora dataset utilizing Planetoid class. Normalize dataset utilizing T.NormalizeFeatures() and transfer it to chose machine.
• Set hyperparameters: hidden_channels, heads, studying fee (lr), and epochs.
• Create GAT mannequin occasion with specified parameters, transfer it to chose machine. Use Adam optimizer with specified lr and weight decay.
• Outline prepare() and take a look at() capabilities for mannequin coaching and analysis. prepare() performs a single iteration, calculates loss with cross-entropy, and updates parameters utilizing backpropagation. take a look at() evaluates mannequin accuracy on coaching, validation, and take a look at units.
• Iterate over epochs, prepare mannequin, and consider efficiency on validation set. Replace greatest validation and corresponding take a look at accuracy if new greatest is discovered. Print coaching and validation metrics for every epoch.
• Calculate and print median time per epoch at coaching finish to measure pace.

Graph Pooling and Graph Classification

Graph Pooling and Graph Classification are important elements and duties in Graph Neural Networks (GNNs) for dealing with graph-structured information. I received’t go into a lot particulars however let’s break down these ideas:

Graph Pooling

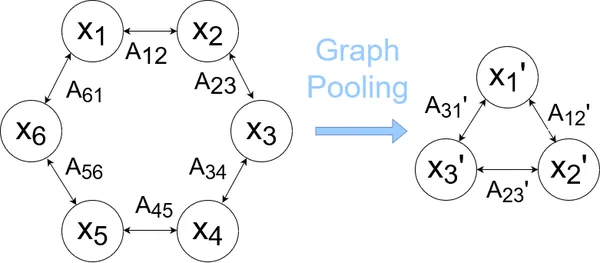
Graph pooling is a method used to down pattern or scale back the scale of a graph whereas preserving its essential structural and relational info. It’s analogous to pooling layers in convolutional neural networks (CNNs) used for picture information.

Pooling is employed to mixture info from teams of nodes and edges within the graph, lowering computational complexity and enhancing the mannequin’s capacity to be taught hierarchical representations. There are numerous graph pooling strategies, together with graph coarsening, hierarchical clustering, and attention-based pooling. These strategies goal to retain essential graph constructions and options whereas discarding much less related info.

Instance

In a hierarchical pooling strategy, the graph is recursively coarsened by merging nodes or aggregating neighborhoods till a desired measurement or stage of abstraction is reached. This course of permits the mannequin to seize each native and world graph constructions effectively.

Graph Classification

Graph classification is a job by which a complete graph is assigned a single label or class based mostly on its structural and have info. It’s a elementary downside in graph analytics and has functions in varied domains equivalent to bioinformatics, social community evaluation, and cheminformatics. 

The purpose of graph classification is to be taught discriminative representations of graphs that seize their inherent properties and traits, enabling correct prediction of their labels. Graph classification strategies sometimes contain extracting significant options from graphs utilizing methods equivalent to graph embedding, graph neural networks, or graph kernels. These options are then fed right into a classifier (e.g., a completely linked neural community or a assist vector machine) to foretell the graph labels.

Instance

In a molecular graph classification job, every graph represents a molecule, and the duty is to foretell the molecule’s bioactivity or drug-likeness based mostly on its chemical construction. Graph neural networks can be utilized to be taught representations of molecules from their graph constructions and atom options, that are then used for classification.

So, in abstract, graph pooling methods allow environment friendly down sampling of graphs whereas preserving essential structural info, whereas graph classification strategies goal to be taught representations of whole graphs for correct prediction of their labels. These elements play essential roles in enabling GNNs to deal with graph-structured information successfully and carry out varied duties equivalent to node classification, hyperlink prediction, and graph classification throughout various domains.

Purposes of GNNs

Graph Neural Networks (GNNs) have discovered functions throughout varied domains on account of their capacity to mannequin complicated relationships and dependencies in information represented as graphs. Some examples of making use of GNNs in real-world situations are:-

• Fraud Detection: Fraud detection is a essential job in varied industries equivalent to finance, insurance coverage, and e-commerce. GNNs may be utilized to detect fraudulent actions by modeling the relationships between entities (e.g., customers, transactions) in a graph.
• Suggestion Techniques: Suggestion methods goal to foretell customers’ preferences or pursuits in objects (e.g., motion pictures, merchandise) based mostly on their interactions. GNNs can seize the complicated relationships between customers and objects in a graph to generate correct suggestions.
• Drug Discovery: In drug discovery, GNNs can mannequin the molecular construction of compounds and predict their properties or interactions with organic targets. This allows extra environment friendly drug screening and lead optimization processes.

Challenges in Implementing and Scaling GNNs

• Graph Measurement: Scaling GNNs to giant graphs with tens of millions of nodes and edges poses computational challenges.
• Heterogeneous Knowledge: Dealing with graphs with heterogeneous node and edge attributes requires specialised methods.
• Interpretability: Decoding the predictions of GNNs and understanding the discovered representations stay difficult.

Conclusion

Graph Neural Networks (GNNs) have emerged as highly effective instruments for modeling and analyzing graph-structured information throughout varied domains. From fraud detection and advice methods to drug discovery, GNNs provide versatile options to complicated issues. Regardless of challenges, ongoing analysis and developments proceed to broaden the capabilities and functions of GNNs, making them indispensable instruments for information scientists and researchers alike. By understanding the rules and functions of GNNs, practitioners can leverage these methods to deal with real-world challenges successfully.

Key Takeaways

• GNNs provide a strong framework for analysing and studying from graph-structured information.
• They’re relevant in varied real-world situations equivalent to social community evaluation, advice methods, fraud detection, and drug discovery.
• Understanding the basics of GNNs, together with graph illustration, message passing, and graph convolutional networks (GCNs), is essential for efficient implementation.
• Superior ideas like Graph Consideration Networks (GATs), and graph pooling methods additional improve the capabilities of GNNs in capturing complicated patterns in graphs.
• Sensible examples and code snippets show learn how to apply GNNs to unravel real-world issues, showcasing their effectiveness and sensible utility.
• Challenges in implementing and scaling GNNs exist, however ongoing analysis focuses on addressing these challenges and enhancing the scalability and interpretability of GNNs.
• Readers are inspired to discover additional and experiment with GNNs in their very own tasks, leveraging out there assets and documentation to drive innovation and handle sensible challenges.

Ceaselessly Requested Questions

References

The media proven on this article just isn’t owned by Analytics Vidhya and is used on the Creator’s discretion.