Mastering Decoder-Solely Transformer: A Complete Information

Introduction

On this weblog put up, we’ll discover the Decoder-Solely Transformer structure, which is a variation of the Transformer mannequin primarily used for duties like language translation and textual content technology. The Decoder-Solely Transformer consists of a number of blocks stacked collectively, every containing key elements equivalent to masked multi-head self-attention and feed-forward transformations.

Studying Targets

•  Discover the structure and elements of the Decoder-Solely Transformer mannequin.
• Perceive the position of consideration mechanisms, together with Scaled Dot-Product Consideration and Masked Self-Consideration, within the mannequin.
•  Study the significance of positional embeddings and normalization strategies in transformer fashions.
• Focus on the usage of feed-forward transformations and residual connections in enhancing coaching stability and effectivity.

Elements of Decoder-Solely Transformer Blocks

Let’s delve into these elements and the general construction of the mannequin.

Scaled Dot-Product Consideration

This can be a essential mechanism inside every transformer block, figuring out consideration scores based mostly on token similarity within the sequence. These scores are then utilized to judge the importance of every token in producing the output.

Tokens

Understanding consideration begins with the enter to a self-attention layer, which consists of a batch of token sequences. Every token is represented by a vector within the sequence, assuming a batch dimension of b and a sequence size of max_len. The self-attention layer receives a tensor of form [ batch-size, seq_len, token dimensionality ]. 

Self-attention Layer Inputs  

It employs three linear layers for question, key, and worth, reworking the enter into key, vector, and worth sequences. These linear layers contain matrix multiplication with the important thing, question, and worth elements.

Consideration Scores are generated by evaluating the important thing and question vectors. The eye rating[i,j] measures the affect of token j on the brand new illustration of token i in a sequence. Scores are computed by way of dot product of question vector for token i and key vector for token j.

The multiplication of the question with the transposed key matrix yields an consideration matrix of dimension [ seq_len,seq_len ], containing pairwise consideration scores within the sequence. Matrix is split by sqrt(d) for stability, adopted by softmax for legitimate likelihood distributions.

Worth Vectors are then decided based mostly on the eye scores, making a weighted mixture of worth vectors for every token. Taking the dot product of the eye matrix with the worth matrix produces a d-dimensional output vector for every token within the enter sequence.

Implementation with Code

import torch
import torch.nn.practical as F

# Assume enter tensors
batch_size = 32
seq_len = 10
token_dim = 64
d = token_dim  # Dimensionality of tokens

# Generate random enter tensor
input_tensor = torch.randn(batch_size, seq_len, token_dim)
# Linear layers for question, key, and worth
query_layer = torch.nn.Linear(token_dim, d)
key_layer = torch.nn.Linear(token_dim, d)
value_layer = torch.nn.Linear(token_dim, d)

# Apply linear transformations
question = query_layer(input_tensor)
key = key_layer(input_tensor)
worth = value_layer(input_tensor)

# Compute consideration scores
scores = torch.matmul(question, key.transpose(-2, -1))  # Dot product of question and key
scores /= torch.sqrt(torch.tensor(d, dtype=torch.float32))  # Scale by sq. root of d

# Apply softmax to get consideration weights
attention_weights = F.softmax(scores, dim=-1)
# Weighted sum of worth vectors based mostly on consideration weights
weighted_sum = torch.matmul(attention_weights, worth)
print(weighted_sum)

Masked Self-Consideration

Throughout coaching, the decoder adjusts self-attention to stop tokens from attending to future tokens, making certain autoregressive output technology with out data leakage. This modified self-attention, often known as masked self-attention, is a variant that selectively consists of tokens within the consideration computation whereas excluding future tokens based mostly on their place within the sequence.

Contemplate a token sequence [‘you’, ‘are’, ‘making’, ‘progress’, ‘.’]. If we deal with computing consideration scores for the token ‘are’, masked self-attention solely considers tokens previous ‘making’ within the sequence, equivalent to ‘you’ and ‘are’, whereas excluding ‘progress’ and ‘.’. This restriction ensures that in self-attention, the mannequin can’t entry data from tokens forward within the sequence.

To implement masked self-attention, after multiplying the question and key matrices, we receive an consideration matrix of dimension [seq_len, seq_len], containing consideration scores for every token pair within the sequence. Earlier than making use of the softmax operation row-wise to this matrix, we set all values above the diagonal (representing future tokens) to unfavourable infinity. This manipulation ensures that in softmax, tokens can solely attend to earlier or present tokens, successfully masking out any data from future tokens. Consequently, the eye scores are adjusted to exclude tokens that observe a given token within the sequence.

Consideration

The eye mechanism we’ve mentioned makes use of softmax to normalize consideration scores throughout the sequence, forming a sound likelihood distribution. This strategy can result in consideration being dominated by just a few phrases. Thus limiting the mannequin’s skill to deal with a number of positions inside the sequence. To handle this, we divide the eye into a number of heads. Every head performs the masked consideration operation independently however with separate key, question, and worth projections.

Multiheaded self-attention makes use of separate projections for every head to cut back computational prices by decreasing the dimensionality of key, question, and worth vectors from d to d//H, the place H represents the variety of heads. This enables every head to study distinctive representational subspaces and deal with totally different components of the sequence, whereas mitigating computational bills. The output of every head might be mixed by means of concatenation, averaging, or projection. The concatenated output from all consideration heads maintains a dimension of d, the identical because the enter dimension of the eye layer.

Implementation with Code

import torch
import torch.nn.practical as F

class MultiheadSelfAttention(torch.nn.Module):a
   def __init__(self, d_model, num_heads):
       tremendous(MultiheadSelfAttention, self).__init__()
       assert d_model % num_heads == 0, "d_model should be divisible by num_heads"
       self.d_model = d_model
       self.num_heads = num_heads
       self.head_dim = d_model // num_heads

       self.query_linear = torch.nn.Linear(d_model, d_model)
       self.key_linear = torch.nn.Linear(d_model, d_model)
       self.value_linear = torch.nn.Linear(d_model, d_model)

       self.concat_linear = torch.nn.Linear(d_model, d_model)


   def ahead(self, x, masks=None):
       batch_size, seq_len, _ = x.dimension()

       # Linear projections for question, key, and worth
       question = self.query_linear(x)  # Form: [batch_size, seq_len, d_model]
       key = self.key_linear(x)  # Form: [batch_size, seq_len, d_model]
       worth = self.value_linear(x)  # Form: [batch_size, seq_len, d_model]

       # Reshape question, key, and worth to separate into a number of heads
       question = question.view(batch_size, seq_len, self.num_heads, self.head_dim).permute(0, 2, 1, 3)  # Form: [batch_size, num_heads, seq_len, head_dim]
       key = key.view(batch_size, seq_len, self.num_heads, self.head_dim).permute(0, 2, 1, 3)  # Form: [batch_size, num_heads, seq_len, head_dim]
       worth = worth.view(batch_size, seq_len, self.num_heads, self.head_dim).permute(0, 2, 1, 3)  # Form: [batch_size, num_heads, seq_len, head_dim]

       # Compute consideration scores
       scores = torch.matmul(question, key.permute(0, 1, 3, 2)) / torch.sqrt(torch.tensor(self.head_dim, dtype=torch.float32))  # Form: [batch_size, num_heads, seq_len, seq_len]

       # Apply masks to stop attending to future tokens
       if masks is just not None:
           scores.masked_fill_(masks == 0, float('-inf'))

       # Apply softmax to get consideration weights
       attention_weights = F.softmax(scores, dim=-1)  # Form: [batch_size, num_heads, seq_len, seq_len]

       # Weighted sum of worth vectors based mostly on consideration weights
       context = torch.matmul(attention_weights, worth)  # Form: [batch_size, num_heads, seq_len, head_dim]


       # Reshape and concatenate consideration heads
       context = context.permute(0, 2, 1, 3).contiguous().view(batch_size, seq_len, -1)  # Form: [batch_size, seq_len, num_heads * head_dim]
       output = self.concat_linear(context)  # Form: [batch_size, seq_len, d_model]


       return output, attention_weights


# Instance utilization and testing
batch_size = 2
seq_len = 5
d_model = 64
num_heads = 4

# Generate random enter tensor
input_tensor = torch.randn(batch_size, seq_len, d_model)
# Create MultiheadSelfAttention module
consideration = MultiheadSelfAttention(d_model, num_heads)


# Ahead move
output, attention_weights = consideration(input_tensor)

# Print shapes
print("Enter Form:", input_tensor.form)
print("Output Form:", output.form)
print("Consideration Weights Form:", attention_weights.form)

Construction of Every Block

Now we’ll dive deeper into the construction of every block.

Residual Connections

Residual connections are a important facet of transformer blocks, surrounding the elements inside every block. They facilitate the circulate of gradients throughout coaching by preserving data from earlier layers. Every transformer block usually provides a residual connection between its self-attention and feed-forward sub-layers.

As an alternative of merely passing the neural community activation by means of a layer, we make use of a residual connection by storing the enter to the layer, computing the layer output, after which including the layer enter to the layer’s output. This course of ensures that the dimension of the enter stays unchanged.

Residual connections play an important position in addressing points like vanishing and exploding gradients, contributing to the soundness and effectivity of the coaching course of. They act as a “shortcut” that enables gradients to circulate freely by means of the community throughout backpropagation, thereby enhancing coaching ease and stability.

Implementation with Code

import torch
import torch.nn as nn

class ResidualBlock(nn.Module):
   def __init__(self, sublayer):
       tremendous(ResidualBlock, self).__init__()
       self.sublayer = sublayer

   def ahead(self, x):
       # Cross enter by means of sublayer
       sublayer_output = self.sublayer(x)

       # Add residual connection
       output = x + sublayer_output
      return output

# Instance utilization
input_size = 512
output_size = 512  # Match the enter dimension for the linear layer

# Outline a easy sub-layer (e.g., linear transformation)
sublayer = nn.Linear(input_size, output_size)


# Create a residual block with the sub-layer
residual_block = ResidualBlock(sublayer)

# Generate a random enter tensor
input_tensor = torch.randn(1, input_size)

# Ahead move by means of the residual block
output_tensor = residual_block(input_tensor)

# Print shapes for illustration
print("Enter Form:", input_tensor.form)
print("Output Form:", output_tensor.form)

Layer Normalization

Layer normalization is essential in stabilizing coaching inside every sub-layer (equivalent to consideration and feed-forward layers) of a transformer block. Two widespread normalization strategies are batch normalization and layer normalization. Each strategies rework activation values utilizing a normal equation.

To acquire the normalized activation worth, we subtract the imply and divide by the usual deviation of the unique activation worth. Batch normalization calculates a imply and customary deviation per dimension over all the mini-batch, therefore its identify.

Layer normalization in a Decoder-Solely transformer includes computing the imply and customary deviation over the enter’s ultimate dimension, eliminating dependency on the batch dimension and enhancing coaching stability by computing normalization statistics over the embedding dimension. Affine transformation is a typical follow in deep neural networks, notably with normalization layers. It includes normalizing the activation worth utilizing layer normalization and adjusting it additional utilizing a relentless multiplier and additive fixed, that are learnable parameters.

In a cake recipe, the normalization layer prepares the batter, whereas the affine transformation customizes the style and texture. The constants γ and β act because the sugar and butter, making small changes to the normalized values to enhance the neural community’s total efficiency.

Layer normalization employs a modified customary deviation with a small fixed (ε) within the denominator to stop points like dividing by zero and preserve stability.

Implementation with Code

import torch
import torch.nn as nn


class LayerNormalization(nn.Module):
   def __init__(self, options, eps=1e-6):
       tremendous(LayerNormalization, self).__init__()
       self.gamma = nn.Parameter(torch.ones(options))
       self.beta = nn.Parameter(torch.zeros(options))
       self.eps = eps


   def ahead(self, x):
       imply = x.imply(dim=-1, keepdim=True)
       std = x.std(dim=-1, keepdim=True)
       x_normalized = (x - imply) / (std + self.eps)
       output = self.gamma * x_normalized + self.beta
       return output


# Instance utilization
input_size = 512
batch_size = 10


# Create a layer normalization occasion
layer_norm = LayerNormalization(input_size)


# Generate a random enter tensor
input_tensor = torch.randn(batch_size, input_size)


# Ahead move by means of layer normalization
output_tensor = layer_norm(input_tensor)


# Print shapes and outputs for illustration
print("Enter Form:", input_tensor.form)
print("Output Form:", output_tensor.form)
print("Output Imply:", output_tensor.imply().merchandise())
print("Output Normal Deviation:", output_tensor.std().merchandise())

Feed-Ahead Transformation

In a decoder-only transformer block, there’s a step after the eye mechanism referred to as the pointwise feed-forward transformation. This course of includes passing every token vector by means of a small feed-forward neural community, which consists of two linear layers separated by an activation operate.

When selecting an activation operate for the feed-forward layers in a big language mannequin , it’s essential to contemplate efficiency. After evaluating numerous activation features, researchers discovered that the SwiGLU activation operate delivers the very best outcomes given a hard and fast computational funds.
SwiGLU is broadly favored and generally utilized in fashionable giant language fashions (LLMs) due to its effectiveness.

Establishing the Decoder-Solely Transformer Mannequin

We’ll now assemble the decoder-only transformer mannequin.

Step1: Mannequin Inputs Development

Token Embedding:

Token embeddings are important in capturing the that means of phrases or tokens inside a decoder-only transformer mannequin. Textual content undergoes tokenization, adopted by conversion into high-dimensional embedding vectors by means of an embedding layer inside the mannequin.

The embedding layer features like a desk, assigning every token a novel integer index from the vocabulary. This index corresponds to a row within the embedding matrix, which has dimensions d columns and V rows (V is the dimensions of our vocabulary). By wanting up the token’s index on this matrix, we get its d-dimensional embedding.

Throughout coaching, the mannequin adjusts these embeddings based mostly on the information it sees, permitting it to study higher representations of phrases over time. It’s just like the mannequin is studying to know phrases higher because it sees extra examples, enhancing its efficiency.

Positional Embedding

Positional embeddings play an important position in transformer fashions by offering important details about the order of tokens in a sequence. Not like recurrent or convolutional fashions, transformers lack inherent data of token order, making positional embeddings essential for understanding sequence construction.

One widespread methodology includes including positional embeddings to every token within the enter sequence. These embeddings have the identical dimensionality as token embeddings (typically denoted as d) and are trainable, that means they modify throughout coaching. Their function is to assist the mannequin differentiate tokens based mostly on their positions within the sequence, enhancing the mannequin’s skill to know and course of sequential information precisely.

Implementation with Code

import torch
import torch.nn as nn


class PositionalEncoding(nn.Module):
   def __init__(self, d_model, max_len=512):
       tremendous(PositionalEncoding, self).__init__()
       self.d_model = d_model
       self.max_len = max_len

       # Create a positional encoding matrix
       pe = torch.zeros(max_len, d_model)
       place = torch.arange(0, max_len, dtype=torch.float32).unsqueeze(1)
       div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-torch.log(torch.tensor(10000.0)) / d_model))
       pe[:, 0::2] = torch.sin(place * div_term)
       pe[:, 1::2] = torch.cos(place * div_term)
       pe = pe.unsqueeze(0)

       self.register_buffer('pe', pe)

   def ahead(self, x)
       # Add positional embeddings to enter token embeddings
       x = x + self.pe[:, :x.size(1)]

      return x

# Instance utilization
d_model = 512  # Dimensionality of token embeddings and positional embeddings
max_len = 100  # Most sequence size

# Create a positional encoding occasion
positional_encoding = PositionalEncoding(d_model, max_len)

# Generate a random enter token embedding tensor
input_token_embeddings = torch.randn(1, max_len, d_model)

# Ahead move by means of positional encoding
output_embeddings = positional_encoding(input_token_embeddings)

# Print shapes for illustration
print("Enter Token Embeddings Form:", input_token_embeddings.form)
print("Output Token Embeddings Form:", output_embeddings.form)

Methods for Positional Embeddings

There are two foremost methods for producing positional embeddings:

• Discovered Positional Embeddings: Positional embeddings, akin to token embeddings, can reside in an embedding layer and study from information throughout coaching. This strategy is simple to implement however could not generalize nicely to longer sequences than these seen throughout coaching.
• Mounted Positional Embeddings: These will also be created utilizing mathematical features like sine and cosine, as outlined within the textual content. These features create embeddings based mostly on the token’s absolute place within the sequence. Whereas this strategy is extra generalizable, it requires defining a rule or equation for producing positional embeddings.

General, positional embeddings are important for transformers to know the sequential order of tokens, enabling them to course of textual content and different sequential information successfully.

Step2: Mannequin Physique

The enter sequence sequentially passes by means of a number of decoder-only transformer blocks.

In a decoder-only transformer mannequin, after developing the enter by including positional embeddings to token embeddings, it passes by means of a sequence of transformer blocks. The variety of these blocks relies on the dimensions of the mannequin.

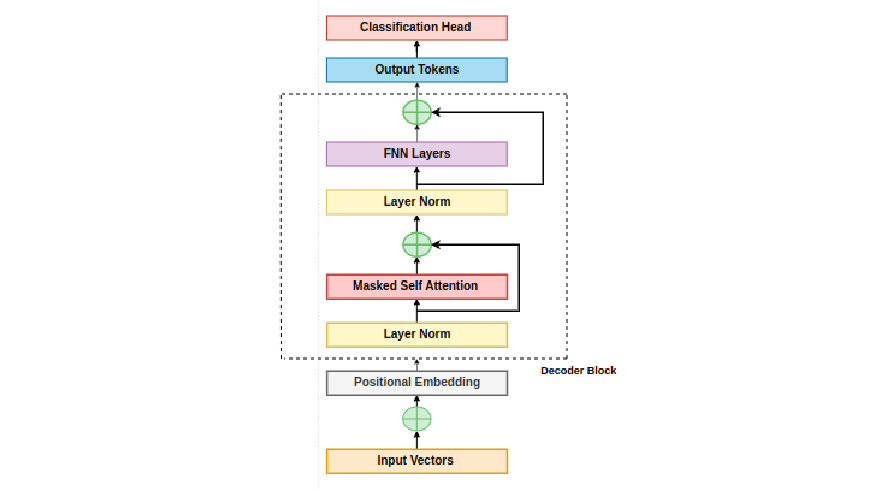
Mannequin Structure 

Rising the mannequin’s dimension might be achieved by both rising the variety of transformer blocks (layers) or by rising the dimensionality (d) of token embeddings. Rising d results in bigger weight matrices in consideration and feed-forward layers. Usually, scaling up a decoder-only transformer mannequin includes rising each the variety of layers and the hidden dimension.

Rising the mannequin’s parameters is achieved by rising the variety of consideration heads inside every consideration layer. However this doesn’t straight have an effect on the variety of parameters if every consideration head has a dimension of d.

Step3: Classification

A classification head predicts the following token within the sequence or performs textual content technology duties. Within the decoder-only transformer structure, after passing the enter sequence by means of the mannequin’s physique and acquiring a sequence of token vectors, we convert every token vector right into a likelihood distribution over potential subsequent tokens. This course of includes including an additional linear layer with enter dimension d and output dimension V to the tip of the mannequin, making a classification head.

Utilizing this linear layer, we will generate a likelihood distribution for every token within the output sequence, enabling us to carry out duties equivalent to:

• Subsequent Token Prediction: That is the pretraining goal the place the mannequin learns to foretell the following token for every token within the enter sequence utilizing a cross-entropy loss operate.
• Inference: By sampling from the token distribution generated by the mannequin, we will autoregressively decide the very best subsequent token, which is beneficial for textual content technology duties.

The classification head permits textual content technology and predictions utilizing realized token chances.

After processing our enter by means of all decoder-only transformer blocks, we’ve got two choices. The primary is to move all output token embeddings by means of a linear classification layer, enabling us to use a subsequent token prediction loss throughout all the sequence, usually completed throughout pretraining. The second choice includes passing solely the ultimate output token by means of the linear classification layer. Permitting for the sampling of the following token throughout inference.

Implementation with Code

import torch
import torch.nn as nn

class ClassificationHead(nn.Module):
   def __init__(self, input_size, vocab_size):
       tremendous(ClassificationHead, self).__init__()
       self.linear = nn.Linear(input_size, vocab_size)

   def ahead(self, x):
       # Cross token embeddings by means of linear layer
       output_logits = self.linear(x)
       return output_logits

# Instance utilization
input_size = 512
vocab_size = 10000  # Instance vocabulary dimension

# Create a classification head occasion
classification_head = ClassificationHead(input_size, vocab_size)

# Generate a random enter token embedding tensor
input_token_embeddings = torch.randn(10, input_size)  # Batch dimension of 10

# Ahead move by means of classification head
output_logits = classification_head(input_token_embeddings)

# Print shapes for illustration
print("Enter Token Embeddings Form:", input_token_embeddings.form)
print("Output Logits Form:", output_logits.form)

Conclusion

The Decoder-Solely Transformer structure excels in producing sequential information, notably in pure language duties. Its key elements, together with token embeddings, positional embeddings, normalization strategies, and the classification head, work collectively to seize semantics, perceive token order, guarantee coaching stability, and allow duties like textual content technology. With its versatility and effectiveness, the Decoder-Solely Transformer stands as a robust instrument in pure language processing purposes.

Key Takeaways

• The Decoder-Solely Transformer, a variant of the Transformer mannequin, performs duties like language translation and textual content technology.
•  Elements equivalent to consideration mechanisms, positional embeddings, normalization strategies, feed-forward transformations, and residual connections are essential for the mannequin’s effectiveness.
• Token embeddings map tokens to high-dimensional areas, capturing semantic data.
•  Positional embeddings present positional data to know token order in sequences.
• Layer normalization and affine transformations contribute to coaching stability and efficiency.
•  The classification head permits duties like subsequent token prediction and textual content technology.
• Examine token embeddings and their significance in capturing semantic data within the mannequin.
• Study the classification head’s position in subsequent token prediction and textual content technology within the Decoder-Solely Transformer.

Ceaselessly Requested Questions